A data sample, or subset of a larger population, is used to help understand the behavior and characteristics of the entire population. In the investing world, for example, all of the familiar stock market averages are samples designed to represent the broader stock market and indicate its performance return. For the domestic publicly-traded stock market, populated with at least 10,000 or more companies, the Dow Jones Industrial Average (DJIA) has just 30 representatives.
the S&P 500 has 500. Yet these samples are taken as valid indicators of the broader population. It's important to understand the mechanics of sampling and estimating, particularly as they apply to financial variables, and have the insight to critique the quality of research derived from sampling efforts.
BASICS
Simple Random Sampling
To begin the process of drawing samples from a larger population, an analyst must craft a sampling plan, which indicates exactly how the sample was selected. With a large population, different samples will yield different results, and the idea is to create a consistent and unbiased approach. Simple random sampling is the most basic approach to the problem.
It draws a representative sample with the principle that every member of the population must have an equal chance of being selected. The key to simple random sampling is assuring randomness when drawing the sample. This requirement is achieved a number of ways, most rigorously by first coding every member of the population with a number, and then using a random number generator to choose a subset.
Sometimes it is impractical or impossible to label every single member of an entire population, in which case systematic sampling methods are used. For example, take a case where we wanted to research whether the S&P 500 companies were adding or laying off employees, but we didn't have the time or resources to contact all 500 human resources departments. We do have the time and resources for an in-depth study of a 25-company sample.
A systematic sampling approach would be to take an alphabetical list of the S&P 500 and contact every 25th company on the list, i.e. companies #25, #50, #75, etc., up until #500. This way we end up with 25 companies and it was done under a system that's approximately random and didn't favor a particular company or industry.
Sampling Error
Suppose we polled our 25 companies and came away with a conclusion that the typical S&P 500 firm will be adding approximately 5% to their work force this fiscal year, and, as a result, we are optimistic about the health of the economy. However, the daily news continues to indicate a fair number of layoffs at some companies and hiring freezes at other firms, and we wonder whether this research has actually done its job. In other words, we suspect sampling error: the difference between the statistic from our sample (5% job growth) and the population parameter we were estimating (actual job growth).
Sampling Distribution
A sampling distribution is analogous to a population distribution: it describes the range of all possible values that the sampling statistic can take. In the assessment of the quality of a sample, the approach usually involves comparing the sampling distribution to the population distribution. We expect the sampling distribution to be a pattern similar to the population distribution - that is, if a population is normally distributed, the sample should also be normally distributed. If the sample is skewed when we were expecting a normal pattern with most of the observations centered around the mean, it indicates potential problems with the sample and/or the methodology.
Stratified Random Sampling.
In a stratified random approach, a population is first divided into subpopulations or strata, based upon one or more classification criteria. Within each stratum, a simple random sample is taken from those members (the members of the subpopulation).
The number to be sampled from each stratum depends on its size relative to the population - that is, if a classification system results in three subgroups or strata, and Group A has 50% of the population, and Group B and Group C have 25% each, the sample we draw must conform to the same relative sizes (half of the sample from A, a quarter each from B and C). The samples taken from each strata are then pooled together to form the overall sample.
The table below illustrates a stratified approach to improving our economic research on current hiring expectations. In our earlier approach that randomly drew from all 500 companies, we may have accidentally drawn too heavily from a sector doing well, and under-represented other areas. In stratified random sampling, each of the 500 companies in the S&P 500 index is assigned to one of 12 sectors. Thus we have 12 strata, and our sample of 25 companies is based on drawing from each of the 12 strata, in proportions relative to the industry weights within the index.
The S&P weightings are designed to replicate the domestic economy, which is why financial services and health care (which are relatively more important sectors in today's economy) are more heavily weighted than utilities.
Within each sector, a random approach is used - for example, if there are 120 financial services companies and we need five financial companies for our research study, those five would be selected via a random draw, or by a systematic approach (i.e. every 24th company on an alphabetical list of the subgroup).
Sector | Percent of S&P 500 | Companies to sample | Sector | Percent of S&P 500 | Companies to sample | ||
Business Svcs | 3.8% | 1 | Health Care | 13.6% | 4 | ||
Consumer Goods | 9.4% | 2 | Idstrl Mtls. | 12.7% | 3 | ||
Consumer Svcs | 8.2% | 2 | Media | 3.7% | 1 | ||
Energy | 8.5% | 2 | Software | 3.9% | 1 | ||
Financial Svcs | 20.1% | 5 | Telecomm | 3.2% | 1 | ||
Hardware | 9.4% | 2 | Utilities | 3.4% | 1 | ||
Time-Series Data
Time series date refers to one variable taken over discrete, equally spaced periods of time. The distinguishing feature of a time series is that it draws back on history to show how one variable has changed. Common examples include historical quarterly returns on a stock or mutual fund for the last five years, earnings per share on a stock each quarter for the last ten years or fluctuations in the market-to-book ratio on a stock over a 20-year period. In every case, past time periods are examined.
Cross-Sectional Data
Cross section data typically focuses on one period of time and measures a particular variable across several companies or industries. A cross-sectional study could focus on quarterly returns for all large-cap value mutual funds in the first quarter of 2005, or this quarter's earnings-per-share estimates for all pharmaceutical firms, or differences in the current market-to-book ratio for the largest 100 firms traded on the NYSE. We can see that the actual variables being examined may be similar to a time-series analysis, with the difference being that a single time period is the focus, and several companies, funds, etc. are involved in the study. The earlier example of analyzing hiring plans at S&P 500 companies is a good example of cross-sectional research.
The Central Limit Theorem The central limit theorem
states that, for a population distribution with mean = μ and a finite variance σ2, the sampling distribution will take on three important characteristics as the sample size becomes large:
- The sample mean will be approximately normally distributed.
- The sample mean will be equal to the population mean (μ).
- The sample variance will be equal to the population variance (σ2) divided by the size of the sample (n).
The first assumption - that the sample distribution will be normal - holds regardless of the distribution of the underlying population. Thus the central limit theorem can help make probability estimates for a sample of a non-normal population (e.g. skewed, lognormal), based on the fact that the sample mean for large sample sizes will be a normal distribution. This tendency toward normally distributed series for large samples gives the central limit theorem its most powerful attribute. The assumption of normality enables samples to be used in constructing confidence intervals and to test hypotheses, as we will find when covering those subjects.
Exactly how large is large in terms of creating a large sample? Remember the number 30. According to the reference text, that's the minimum number a sample must be before we can assume it is normally distributed. Don't be surprised if a question asks how large a sample should be - should it be 20, 30, 40, or 50? It's an easy way to test whether you've read the textbook, and if you remember 30, you score an easy correct answer.
Standard Error
The standard error is the standard deviation of the sample statistic. Earlier, we indicated that the sample variance is the population variance divided by n (sample size). The formula for standard error was derived by taking the positive square root of the variance.
If the population standard deviation is given, standard error is calculated by this ratio: population standard deviation / square root of sample size, or σ/(n)1/2. If population standard deviation is unknown, the sample standard deviation (s) is used to estimate it, and standard error = s/(n)1/2. Note that "n" in the denominator means that the standard error becomes smaller as the sample size becomes larger, an important property to remember.
Point Estimate vs. Confidence Interval Population Parameters
A point estimate is one particular value that is used to estimate the underlying population parameter. For example, the sample mean is essentially a point estimate of a population mean. However, because of the presence of sampling error, sometimes it is more useful to start with this point estimate, and then establish a range of values both above and below the point estimate.
Next, by using the probability-numbers characteristic of normally distributed variables, we can state the level of confidence we have that the actual population mean will fall somewhere in our range. This process is knows as "constructing a confidence interval".
The level of confidence we want to establish is given by the number α, or alpha, which is the probability that a point estimate will not fall in a confidence range. The lower the alpha, the more confident we want to be - e.g. alpha of 5% indicates we want to be 95% confident; 1% alpha indicates 99% confidence.
Properties of an Estimator
The three desirable properties of an estimator are that they are unbiased, efficient and consistent:
- Unbiased - The expected value (mean) of the estimate's sampling distribution is equal to the underlying population parameter; that is, there is no upward or downward bias.
- Efficiency - While there are many unbiased estimators of the same parameter, the most efficient has a sampling distribution with the smallest variance.
- Consistency - Larger sample sizes tend to produce more accurate estimates; that is, the sample parameter converges on the population parameter.
The general structure for a (1 - α) confidence interval is given by:
|
Where: the reliability factor increases as a function of an increasing confidence level.
In other words, if we want to be 99% confident that a parameter will fall within a range, we need to make that interval wider than we would if we wanted to be only 90% confident. The actual reliability factors used are derived from the standard normal distribution, or Z value, at probabilities of alpha/2 since the interval is two-tailed, or above and below a point.
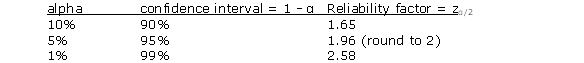 |
Degrees of Freedom
Degrees of freedom are used for determining the reliability-factor portion of the confidence interval with the t-distribution. In finding sample variance, for any sample size n, degrees of freedom = n -
1. Thus for a sample size of 8, degrees of freedom are 7.
For a sample size of 58, degrees of freedom are 57. The concept of degrees of freedom is taken from the fact that a sample variance is based on a series of observations, not all of which can be independently selected if we are to arrive at the true parameter.
One observation essentially depends on all the other observations. In other words, if the sample size is 58, think of that sample of 58 in two parts: (a) 57 independent observations and (b) one dependent observation, on which the value is essentially a residual number based on the other observations. Taken together, we have our estimates for mean and variance. If degrees of freedom is 57, it means that we would be "free" to choose any 57 observations (i.e. sample size - 1), since there is always that 58th value that will result in a particular sample mean for the entire group.
Characteristic of the t-distribution is that additional degrees of freedom reduce the range of the confidence interval, and produce a more reliable estimate. Increasing degrees of freedom is done by increasing sample size. For larger sample sizes, use of the z-statistic is an acceptable alternative to the t-distribution - this is true since the z-statistic is based on the standard normal distribution, and the t-distribution moves closer to the standard normal at higher degrees of freedom.
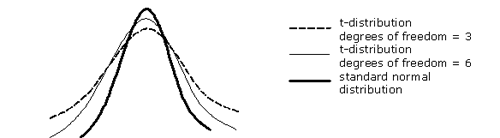
Student's t-distribution
Student's t-distribution is a series of symmetrical distributions, each distribution defined by its degrees of freedom. All of the t-distributions appear similar in shape to a standard normal distribution, except that, compared to a standard normal curve, the t-distributions are less peaked and have fatter tails.
With each increase in degrees of freedom, two properties change: (1) the distribution's peak increases (i.e. the probability that the estimate will be closer to the mean increases), and (2) the tails (in other words, the parts of the curve far away from the mean estimate) approach zero more quickly - i.e. there is a reduced probability of extreme values as we increase degrees of freedom. As degrees of freedom become very large - as they approach infinity - the t-distribution approximates the standard normal distribution.
Figure 2.12: Student's t-distribution
 (See more) Hypothesis Testing |





0 comments:
Post a Comment