While a normally-distributed random variable can have many potential outcomes, the shape of its distribution gives us confidence that the vast majority of these outcomes will fall relatively close to its mean. In fact, we can quantify just how confident we are. By using confidence intervals - ranges that are a function of the properties of a normal bell-shaped curve - we can define ranges of probabilities.
The diagram below has a number of percentages - these numbers (which are approximations and rounded off) indicate the probability that a random outcome will fall into that particular section below the curve.
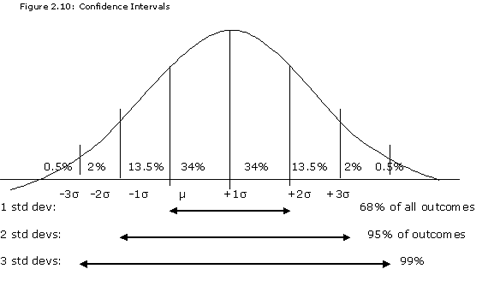 |
In other words, by assuming normal distribution, we are 68% confident that a variable will fall within one standard deviation. Within two standard deviation intervals, our confidence grows to 95%. Within three standard deviations, 99%. Take an example of a distribution of returns of a security with a mean of 10% and a standard deviation of 5%:
- 68% of the returns will be between 5% and 15% (within 1 standard deviation, 10 + 5).
- 95% of the returns will be between 0% and 20% (within 2 std. devs., 10 + 2*5).
- 99% of the returns will be between -5% and 25% (within 3 std. devs., 10 + 3*5)
Standard normal distribution is defined as a normal distribution where mean = 0 and standard deviation = 1. Probability numbers derived from the standard normal distribution are used to help standardize a random variable - i.e. express that number in terms of how many standard deviations it is away from its mean.
Standardizing a random variable X is done by subtracting X from the mean value (μ), and then dividing the result by the standard deviation (σ). The result is a standard normal random variable which is denoted by the letter Z.
| Formula 2.31 Z = (X - μ)/σ |
Example 1:If a distribution has a mean of 10 and standard deviation of 5, and a random observation X is -2, we would standardize our random variable with the equation for Z.
Z = (X - μ)/ σ = (-2 - 10)/5 = -12/5 = -2.4
The standard normal random variable Z tells us how many standard deviations the observation is from the mean. In this case, -2 translates to 2.4 standard deviations away from 10.
Example 2:
You are considering an investment portfolio with an expected return of 10% and a standard deviation of 8%. The portfolio's returns are normally distributed. What is the probability of earning a return less than 2%?
Again, we'd start with standardizing random variable X, which in this case is 10%:
Z = (X - μ)/ σ = (2 - 10)/8 = -8/8 = -1.0
Next, one would often consult a Z-table for cumulative probabilities for a standard normal distribution in order to determine the probability. In this case, for Z = -1, P(Z ≤ x) - 0.158655, or 16%.
Therefore, there is a 16% probability of earning a return of less than 2%.
Keep in mind that your upcoming exam will not provide Z-tables, so, how would you solve this problem on test day?
The answer is that you need to remember that 68% of observations fall + 1 standard deviation on a normal curve, which means that 32% are not within one standard deviation. This question essentially asked for probability of more than one standard deviation below, or 32%/2 = 16%. Study the earlier diagram that shows specific percentages for certain standard deviation intervals on a normal curve - in particular, remember 68% for + one away, and remember 95% for + two away.
Shortfall Risk
Shortfall risk is essentially a refinement of the modern-day development of mean-variance analysis, that is, the idea that one must focus on both risk and return as opposed to simply the return. Risk is typically measured by standard deviation, which measures all deviations - i.e. both positive and negative. In other words, positive deviations are treated as if they were equal to negative deviations. In the real world, of course, negative surprises are far more important to quantify and predict with clarity if one is to accurately define risk. Two mutual funds could have the same risk if measured by standard deviation, but if one of those funds tends to have more extreme negative outcomes, while the other had a high standard deviation due to a preponderance of extreme positive surprises, then the actual risk profiles of those funds would be quite different. Shortfall risk defines a minimum acceptable level, and then focuses on whether a portfolio will fall below that level over a given time period.
Roy's Safety-First Ratio
An optimal portfolio is one that minimizes the probability that the portfolio's return will fall below a threshold level. In probability notation, if RP is the return on the portfolio, and RL is the threshold (the minimum acceptable return), then the portfolio for which P(RP < RL) is minimized will be the optimal portfolio according to
| Formula 2.32 SFRatio = (E(RP) - RL)/ σP |
Example:
Let's say our minimum threshold is -2%, and we have the following expectations for portfolios A and B:
| Portfolio A | Portfolio B | |
| Expected Annual Return | 8% | 12% |
| Standard Deviation | 10% | 16% |
Answer: The SFRatio for portfolio A is (8 - (-2))/10 = 1.0
The SFRatio for portfolio B is (12 - (-2))/16 = 0.875
In other words, the minimum threshold is one standard deviation away in Portfolio A, and just 0.875 away in Portfolio B, so by safety-first rules we opt for Portfolio A.
Lognormal Distributions
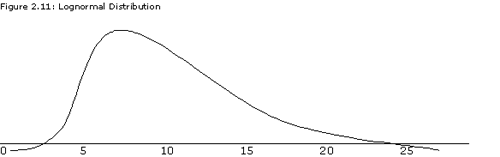
A lognormal distribution has two distinct properties: it is always positive (bounded on the left by zero), and it is skewed to the right. Prices for stocks and many other financial assets (anything which by definition can never be negative) are often found to be lognormally distributed. Also, the lognormal and normal distributions are related: if a random variable X is lognormally distributed, then its natural log, ln(X) is normally distributed. (Thus the term "lognormal" - the log is normal.) Figure 2.11 below demonstrates a typical lognormal distribution.
 |
(See more) Discrete and Continuous Compounding





0 comments:
Post a Comment