Individual Investment
The expected return for an individual investment is simply the sum of the probabilities of the possible expected returns for the investment.
Formula 17.3 Expected Return E(R) = p1R1 + p2R2 + .....+ pnRn Where: pn = the probability the return actually will occur in state n Rn = the expected return for state n |
Example:
For Newco's stock, assume the following potential returns.
Figure 3.3: Expected returns for Newco's stock price in the various states
Scenario Probability Expected Return Worst Case 10% 10% Base Case 80% 14% Best Case 10% 18%
Given the above assumptions, determine the expected return for Newco's stock.
Answer:
E(R) = (0.10)(10%) + (0.80)(14%) + (0.10)(18%)
E(R) = 14.0%
The expected return for Newco's stock is 14%.Portfolio
To determine the expected return on a portfolio, the weighted average expected return of the assets that comprise the portfolio is taken.
Formula 17.4 E(R) of a portfolio = w1R1 + w2Rq + ...+ wnRn |
Assume an investment manager has created a portfolio with the Stock A and Stock B. Stock A has an expected return of 20% and a weight of 30% in the portfolio. Stock B has an expected return of 15% and a weight of 70%. What is the expected return of the portfolio?
Example:
Answer:
E(R) = (0.30)(20%) + (0.70)(15%)
= 6% + 10.5% = 16.5%
The expected return of the portfolio is 16.5%
Computing Variance and Standard Deviation for an Individual
To measure the risk of an investment, both the variance and standard deviation for that investment can be calculated.
To measure the risk of an investment, both the variance and standard deviation for that investment can be calculated.
Formula 17.5 Variance = Where: Pn = probability of occurrence Rn = return in n occurrence E(R) = expected return |
Formula 17.6 Standard Deviation = |
Example: Variance and Standard Deviation of an Investment
Given the following data for Newco's stock, calculate the stock's variance and standard deviation. The expected return based on the data is 14%.
Figure: Expected return for Newco in various states
Scenario Probability Return Expected Return Worst Case 10% 10% 0.01 Base Case 80% 14% 0.112 Best Case 10% 18% 0.018
Answer:
σ2 = (0.10)(0.10 - 0.14)2 + (0.80)(0.14 - 0.14)2 + (0.10)(0.18 - 0.14)2
= 0.0003
The variance for Newco's stock is 0.0003.
Given that the standard deviation of Newco's stock is simply the square root of the variance, the standard deviation is 0.0179 or 1.79%.
Covariance
The covariance is the measure of how two assets relate (move) together. If the covariance of the two assets is positive, the assets move in the same direction.
For example, if two assets have a covariance of 0.50, then the assets move in the same direction. If however the two assets have a negative covariance, the assets move in opposite directions. If the covariance of the two assets is zero, they have no relationship.
Formula 17.7 Covariancea,b= 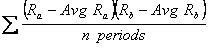 |
Example:
Calculate the covariance between two assets
Assume the mean return on Asset A is 10% and the mean return on Asset B is 15%. Given the following returns over the past 5 periods, calculate the covariance for
Asset A as it relates to Asset B.
Returns
NRa Rb 1 10% 18% 2 15% 25% 3 5% 2% 4 13% 8% 5 8% 17%
Answer:
NRa Rb Ra- Avg Ra Rb-Avg Rb Ra- Avg Ra Rb-Avg Rb 1 10 18 0 3 0 2 15 25 5 10 50 3 5 2 -5 -13 65 4 13 8 3 -7 -21 5 8 17 -2 2 -4
Sum90.00
The covariance would equal 18 (90/5).
Correlation
The correlation coefficient is the relative measure of the relationship between two assets.
It is between +1 and -1, with a +1 indicating that the two assets move completely together and a -1 indicating that the two assets move in opposite directions from each other.
Formula 17.8
Example: Calculate the correlation of Asset A with Asset B.
Given our covariance of 18 in the example above, what is the correlation coefficient for Asset A relative to Asset B if Asset A has a standard deviation of 4 and Asset B has a standard deviation of 3.
Answer:
Correlation coefficient = 18/(8)(4) = 0.563
Components of the Portfolio Standard Deviation Formula
Remember that when calculating the expected return of a portfolio, it is simply the sum of the weighted returns of each asset in the portfolio. Unfortunately, determining the standard deviation of a portfolio, it is not that simple. Not only are the weights of the assets in the portfolio and the standard deviation for each asset in the portfolio needed, the correlation of the assets in the portfolio is also required to determine the portfolio standard deviation.
The equation for the standard deviation for a two asset portfolio is long, but should be memorized for the exam.
Formula 17.9 |





0 comments:
Post a Comment