Skew And Kurtosis

Skew And Kurtosis

SkewSkew, or skewness, can be mathematically defined as the averaged cubed deviation from the mean divided by the standard deviation cubed. If the result of the computation is greater than zero, the distribution is positively skewed.

If it's less than zero, it's negatively skewed and equal to zero means it's symmetric. For interpretation and analysis, focus on downside risk.

Negatively skewed distributions have what statisticians call a long left tail (refer to graphs on previous page), which for investors can mean a greater chance of extremely negative outcomes. Positive skew would mean frequent small negative outcomes, and extremely bad scenarios are not as likely.

A nonsymmetrical or skewed distribution occurs when one side of the distribution does not mirror the other. Applied to investment returns, nonsymmetrical distributions are generally described as being either positively skewed (meaning frequent small losses and a few extreme gains) or negatively skewed (meaning frequent small gains and a few extreme losses).

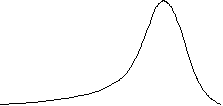Positive Skew	Negative Skew

Figure 2.4

For positively skewed distributions, the mode (point at the top of the curve) is less than the median (the point where 50% are above/50% below), which is less than the arithmetic mean (sum of observations/number of observations). The opposite rules apply to negatively skewed distribution: mode is greater than median, which is greater than arithmetic mean.

Positive: Mean > Median > Mode Negative: Mean < Median < Mode

Notice that by alphabetical listing, it's mean à median à mode. For positive skew, they are separated with a greater than sign, for negative, less than.

Kurtosis  

Kurtosis refers to the degree of peak in a distribution. More peak than normal (leptokurtic) means that a distribution also has fatter tails and that there is a greater chance of extreme outcomes compared to a normal distribution.

The kurtosis formula measures the degree of peak. Kurtosis equals three for a normal distribution; excess kurtosis calculates and expresses kurtosis above or below 3.

In figure 2.5 below, the solid line is the normal distribution; the dashed line is leptokurtic distribution.

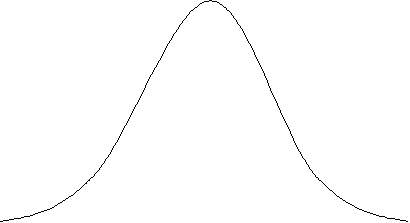Figure 2.5: Kurtosis

Sample Skew and Kurtosis

For a calculated skew number (average cubed deviations divided by the cubed standard deviation), look at the sign to evaluate whether a return is positively skewed (skew > 0), negatively skewed (skew < 0) or symmetric (skew = 0). A kurtosis number (average deviations to the fourth power divided by the standard deviation to the fourth power) is evaluated in relation to the normal distribution, on which kurtosis = 3. Since excess kurtosis = kurtosis - 3, any positive number for excess kurtosis would mean the distribution is leptokurtic (meaning fatter tails and greater risk of extreme outcomes).

(See more) Basic Probability Concepts

| | Print This! | No comments

Do you like this post?